RSS Feed

UNDECIDABILITY

Posted by Jennifer G. Santiago

1. A LANGUAGE THAT IS NOT RECURSIVE ENUMERABLE

In mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-recognizable. It is known as a type-0 language in the Chomsky hierarchy of formal languages. The class of all recursively enumerable languages is called RE.

To prove this we will consider a language consisting a pair (M, w) where:

1. M, a Turing Machine with inputs set {0,1}

2. W a binary string consisting of 0’s and 1’s.

3. M accepts w.

We will make use of three things in this proof and those are

· Enumerated binary strings

· Coded Turing Machine

· Diagonal language

All regular, context-free, context-sensitive and recursive languages are recursively enumerable.

Recursively undecidable problems give examples of recursively enumerable sets that are not recursive. For example, convergence of phi_x(x) is known to be recursively undecidable, where phi_x denotes the Turing machine with Gödel number x. Hence the set of all x for which phi_x(x) is convergent is not recursive. However, this set is recursively enumerable because it is the range of f defined as follows:

f(x)={x if phi_x(x) is convergent; divergent if phi_x(x) is divergent.
(1)

A set A is recursive iff both A and its complement are recursively enumerable. This provides an approach to constructing additional sets that are not recursively enumerable. In particular, the set of all Gödel numbers of total Turing machines is an example of a set which is not recursively enumerable.

The complements of recursively enumerable but not recursive sets are all not recursively enumerable, although complements of sets that are not recursively enumerable are not necessarily recursively enumerable. For instance, the complement of the set of all Gödel numbers of total Turing machines is not recursively enumerable.

One of fundamental properties of recursively enumerable sets is that they could be alternatively defined by domains as opposed to ranges. In particular, a set A is recursively enumerable iff A is the domain of a recursive function.

*a. Enumerating by binary string

We need to assign integers to all binary strings in order to make a relation of binary input with corresponding integer value. For example ε means integer 1, Binary 0 means integer 2, binary 1 means integer 3, binary 00 means integer 4 and binary 01 means integer 5 and so on. The strings should be enumerated, in the sense that these strings should be ordered by length and strings of equal length should be lexicographically ordered. We can refer ith strings as Wi.

*b. Codes for Turing Machine

The second important thing that we require in the process of providing a language not a recursively enumerated is binary codes for Turing Machine. After coding a TM by {0,1} we can represent a complete Turing Machine by a sequence of binary string. We can also represent many Turing Machines with the help of binary strings and to identification of the Turing Machine by M¡. The representation of Turing Machine can be M= (Q,{0,1}, Γ, d, q1, B, F) as binary string. To represent the TM by binary strings we first assign binary strings to9 integers of states, tape symbol and directions L and R. Following are the steps used to represent the TM using binary string:

1.) We will assume set of states Q has the states q1, q2,…qk for some k. The start state will always be the q1 and the accept state will be q2. The Turing Machine always halt after entering and accept state and therefore it requires only one accept state.


2.) The tape symbols are X₁, X₂,…Xm for some m. Input symbol X₁ can be represented by 0, X₂ will be by 1 and X₃ by B, the blank. Other tape symbols can be assigned to the remaining integers arbitrarily.


3.) The direction L is represented by D₁ and R can be represented by D₂. The language represented by this TM M can be equivalently represented as L(M)= Ld.


4.)After representation of state, input and directions by binary strings we can encode transition function δ. Suppose one transition rule is δ (q₁, Xі, Dm) where I, j, k, l and m represents integer. This transitions rule can be represented by a binary string.

*c. Diagonalization Language


As we know that a Turing Machine can be represented by binary string. Hence different Turing Machines can be represented by various binary strings. In other words the ith Turing Machine M¡ whose code is w¡, the ith binary string. To represent various strings corresponding to various TMs we make use of two dimensional arrays ¡ X j. there are many integers that do not correspond to any TM. If w¡ not a valid Turing Machine code then we consider TM M¡ with one state and no transitions. That is, for these values of ¡, the Turing Machine M¡ is such a machine that immediately halts on any input (being one state machine). Thus L (Mi) = 0 if w¡ fails to be valid TM code.

Definition: The diagonalization language, denoted by Ld is a set of strings w¡ such that w¡ is not in L (M¡). Thus Ld consist of all the strings w such that w is not accepted by TM M whose code is w.

1.) Theorem: The diagonalization language Ld is not recursively enumerable language. In other words, there is no such Turing Machine which can accept Ld .


2. UNDECIDABLE PROBLEM THAT IS NOT RE

There are two distinct senses of the word "undecidable" in contemporary use. The first of these is the sense used in relation to Gödel's theorems, that of a statement being neither provable nor refutable in a specified deductive system. The second sense is used in relation to computability theory and applies not to statements but to decision problems, which are countably infinite sets of questions each requiring a yes or no answer. Such a problem is said to be undecidable if there is no computable function that correctly answers every question in the problem set. The connection between these two is that if a decision problem is undecidable (in the recursion theoretical sense) then there is no consistent, effective formal system which proves for every question A in the problem either "the answer to A is yes" or "the answer to A is no".

Because of the two meanings of the word undecidable, the term independent is sometimes used instead of undecidable for the "neither provable nor refutable" sense. The usage of "independent" is also ambiguous, however. Some use it to mean just "not provable", leaving open whether an independent statement might be refuted.

Undecidability of a statement in a particular deductive system does not, in and of itself, address the question of whether the truth value of the statement is well-defined, or whether it can be determined by other means. Undecidability only implies that the particular deductive system being considered does not prove the truth or falsity of the statement. Whether there exist so-called "absolutely undecidable" statements, whose truth value can never be known or is ill-specified, is a controversial point among various philosophical schools.

One of the first problems suspected to be undecidable, in the second sense of the term, was the word problem for groups, first posed by Max Dehn in 1911, which asks if there is a finitely presented group for which no algorithm exists to determine whether two words are equivalent. This was shown to be the case in 1952.

The combined work of Gödel and Paul Cohen has given two concrete examples of undecidable statements (in the first sense of the term): The continuum hypothesis can neither be proved nor refuted in ZFC (the standard axiomatization of set theory), and the axiom of choice can neither be proved nor refuted in ZF (which is all the ZFC axioms except the axiom of choice). These results do not require the incompleteness theorem. Gödel proved in 1940 that neither of these statements could be disproved in ZF or ZFC set theory. In the 1960s, Cohen proved that neither is provable from ZF, and the continuum hypothesis cannot be proven from ZFC.

In 1970, Soviet mathematician Yuri Matiyasevich showed that Hilbert's Tenth Problem, posed in 1900 as a challenge to the next century of mathematicians, cannot be solved. Hilbert's challenge sought an algorithm which finds all solutions of a Diophantine equation. A Diophantine equation is a more general case of Fermat's Last Theorem; we seek the integer roots of a polynomial in any number of variables with integer coefficients. Since we have only one equation but n variables, infinitely many solutions exist (and are easy to find) in the complex plane; the problem becomes difficult (impossible) by constraining solutions to integer values only. Matiyasevich showed this problem to be unsolvable by mapping a Diophantine equation to a recursively enumerable set and invoking Gödel's Incompleteness Theorem.


3. UNDECIDABLE PROBLEM ABOUT TURING MACHINE

In 1936, Alan Turing proved that the halting problem—the question of whether or not a Turing machine halts on a given program—is undecidable, in the second sense of the term. This result was later generalized to Rice's theorem.

In 1973, the Whitehead problem in group theory was shown to be undecidable, in the first sense of the term, in standard set theory.

In 1977, Paris and Harrington proved that the Paris-Harrington principle, a version of the Ramsey theorem, is undecidable in the axiomatization of arithmetic given by the Peano axioms but can be proven to be true in the larger system of second-order arithmetic.

Kruskal's tree theorem, which has applications in computer science, is also undecidable from the Peano axioms but provable in set theory. In fact Kruskal's tree theorem (or its finite form) is undecidable in a much stronger system codifying the principles acceptable on basis of a philosophy of mathematics called predicativism.

Goodstein's theorem is a statement about the Ramsey theory of the natural numbers that Kirby and Paris showed is undecidable in Peano arithmetic.

Gregory Chaitin produced undecidable statements in algorithmic information theory and proved another incompleteness theorem in that setting. Chaitin's theorem states that for any theory that can represent enough arithmetic, there is an upper bound c such that no specific number can be proven in that theory to have Kolmogorov complexity greater than c. While Gödel's theorem is related to the liar paradox, Chaitin's result is related to Berry's paradox.

Douglas Hofstadter gives a notable alternative proof of incompleteness, inspired by Gödel, in his book Gödel, Escher, Bach.

In 2006, researchers Kurtz and Simon, building on earlier work by J.H. Conway in the 1970s, proved that a natural generalization of the Collatz problem is undecidable.



4. POST CORRESPONDENCE PROBLEMS

The Post correspondence problem is an undecidable decision problem that was introduced by Emil Post in 1946.[1] Because it is simpler than the halting problem and the Entscheidungsproblem it is often used in proofs of undecidability.

The input of the problem consists of two finite lists \alpha_{1}, \ldots, \alpha_{N} and \beta_{1}, \ldots, \beta_{N} of words over some alphabet A having at least two symbols. A solution to this problem is a sequence of indices (i_k)_{1 \le k \le K} with K \ge 1 and 1 \le i_k \le N for all k, such that

\alpha_{i_1} \ldots \alpha_{i_K} = \beta_{i_1} \ldots \beta_{i_K}.

The decision problem then is to decide whether such a solution exists or not.

Many variants of PCP have been considered. One reason is that, when one tries to prove undecidability of some new problem by reducing from PCP, it often happens that the first reduction one finds is not from PCP itself but from an apparently weaker version.

  • The condition that the alphabet A have at least two symbols is required since the problem is decidable if A has only one symbol.
  • A simple variant is to fix n, the number of tiles. This problem is decidable if n ≤ 2, but remains undecidable for n ≥ 7. It is unknown whether the problem is decidable for 3 ≤ n ≤ 6.
  • The circular Post correspondence problem asks whether indexes i1,i2,... can be found such that \alpha_{i_1} \cdots \alpha_{i_k} and \beta_{i_1} \cdots \beta_{i_k} are conjugate words, i.e., they are equal modulo rotation. This variant is undecidable.
  • One of the most important variants of PCP is the bounded Post correspondence problem, which asks if we can find a match using no more than k tiles, including repeated tiles. A brute force search solves the problem in time O(2k), but this may be difficult to improve upon, since the problem is NP-complete. Unlike some NP-complete problems like the boolean satisfiability problem, a small variation of the bounded problem was also shown to be complete for RNP, which means that it remains hard even if the inputs are chosen at random (it is hard on average over uniformly distributed inputs)
  • Another variant of PCP is called the marked Post Correspondence Problem, in which each ui must begin with a different symbol, and each vi must also begin with a different symbol. Halava, Hirvensalo, and de Wolf showed that this variation is decidable in exponential time. Moreover, they showed that if this requirement is slightly loosened so that only the two-character prefixes need to differ (the so-called 2-marked Post Correspondence Problem), the problem becomes undecidable again.
  • The Post Embedding Problem is another variant where one looks for indexes i1,i2,...\alpha_{i_1} \cdots \alpha_{i_k} is a (scattered) subword of \beta_{i_1} \cdots \beta_{i_k}. This variant is easily decidable since, when some solutions exist, in particular a length-one solution exists. More interesting is the Regular Post Embedding Problem, a further variant where one looks for solutions that belong to a given regular language (submitted, e.g., under the form of a regular expression on the set {1,...,N}). The Regular Post Embedding Problem is still decidable but, because of the added regular constraint, it has a very high complexity that dominates every multiply-recursive function. such that


0 comments

CHURCH - TURING THESIS

Posted by Jennifer G. Santiago

I. TURING MACHINES

A Turing machine is a theoretical device that manipulates symbols contained on a strip of tape. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside of a computer. The "Turing" machine was described by Alan Turing in 1937,who called it an "a(utomatic)-machine". Turing machines are not intended as a practical computing technology, but rather as a thought experiment representing a computing machine. They help computer scientists understand the limits of mechanical computation.

A Turing machine that is able to simulate any other Turing machine is called a Universal Turing Machine (UTM, or simply a universal machine). A more mathematically-oriented definition with a similar "universal" nature was introduced by Alonzo Church, whose work on lamda calculus intertwined with Turing's in a formal theory of computation known as the Chuch Turing Thesis The thesis states that Turing machines indeed capture the informal notion of effective method in logic and mathematics, and provide a precise definition of an algorithm or 'mechanical procedure'.

* Formal Definition of Turing Machine

A Turing Machine is a 7-tuple (Q,Σ, Γ, δ, q0, qaccept, qreject),where
  • Q is a finite set of states
  • Σ is an input alphabet, ⊔ / ∈ Σ
  • Γ is a tape alphabet, ⊔ ∈ Γ, and Σ ⊂ Γ
  • δ : Q × Γ → (Q ∪ {qaccept, qreject}) × Γ × {L,R} is the transition function
  • q0inQ is the start state
  • qaccept, qreject are the accept and reject states, respectively.

* Examples of Turing Machine

The following table is Turing's very first example (Turing 1937):
"1. A machine can be constructed to compute the sequence 0 1 0 1 0 1..." (0 1 0...)
ConfigurationBehavior
m-configuration
(state)		Tape symbolTape operationsFinal m-configuration
(state)
bblankP0, Rc
cblankRe
eblankP1, Rf
fblankRb

With regard to what actions the machine actually does, Turing (1936) states the following:

"This [example] table (and all succeeding tables of the same kind) is to be understood to mean that for a configuration described in the first two columns the operations in the third column are carried out successively, and the machine then goes over into the m-configuration in the final column."

He makes this very clear when he reduces the above table to a single instruction called "b" (Undecidable p. 120), but his instruction consists of 3 lines. Instruction "b" has three different symbol possibilities {None, 0, 1}. Each possibility is followed by a sequence of actions until we arrive at the rightmost column, where the final m-configuration is "b":

Current m-configuration (instruction)Tape symbolOperations on the tapeFinal m-configuration (instruction)
bNoneP0b
b0R, R, P1b
b1R, R, P0b

As observed by a number of commentators including Turing (1937) himself, (e.g., Post (1936), Post (1947), Kleene (1952), Wang (1954)) the Turing instructions are not atomic — further simplifications of the model can be made without reducing its computational power

Turing proposed that his table be further atomized by allowing only a single print/erase followed by a single tape movement L/R/N. He gives us this example of the first little table converted (Undecidable, p. 127):

Current m-configuration (Turing state)Tape symbolPrint-operationTape-motionFinal m-configuration (Turing state)
q1blankP0Rq2
q2blankP blank, i.e. ERq3
q3blankP1Rq4
q4blankP blank, i.e. ERq1

Turing's statement still implies five atomic operations. At a given instruction (m-configuration) the machine:

  1. observes the tape-symbol underneath the head
  2. based on the observed symbol goes to the appropriate instruction-sequence to use
  3. prints symbol Sj or erases or does nothing
  4. moves tape left, right or not at all
  5. goes to the final m-configuration for that symbol

Because a Turing machine's actions are not atomic, a simulation of the machine must atomize each 5-tuple into a sequence of simpler actions. One possibility — used in the following examples of "behaviors" of his machine — is as follows:

(qi) Test tape-symbol under head: If the symbol is S0 go to qi.01, if symbol S1 go to qi.11, if symbol S2 go to qi.21, etc.
(qi.01) print symbol Sj0 or erase or do nothing then go to qi.02
(qi.02) move tape left or right nor not at all then go to qm0
(qi.11) print symbol Sj1 or erase or do nothing then go to qi.12
(qi.12) move tape left or right nor not at all then go to qm1
(qi.21) print symbol Sj2 or erase or do nothing then go to qi.22
(qi.22) move tape left or right nor not at all then go to qm2
(etc — all symbols must be accounted for)

So-called "canonical" finite state machines do the symbol tests "in parallel"

In the following example of what the machine does, we will note some peculiarities of Turing's models:

"The convention of writing the figures only on alternate squares is very useful: I shall always make use of it." (Undecidable p. 121)

Thus when printing he skips every other square. The printed-on squares are called F-squares; the blank squares in between may be used for "markers" and are called "E-squares" as in "liable to erasure." The F-squares in turn are his "Figure squares" and will only bear the symbols 1 or 0 — symbols he called "figures" (as in "binary numbers").

In this example the tape starts out "blank", and the "figures" are then printed on it. For brevity only the TABLE-states are shown here:

SequenceInstruction identifier    Head             


..................
11..................
22.....0............
33......0...........
44.....1.0..........
51......1.0.........
62.....0.1.0........
73......0.1.0.......
84.....1.0.1.0......
91......1.0.1.0.....
102.....0.1.0.1.0....
113......0.1.0.1.0...
124.....1.0.1.0.1.0..
131......1.0.1.0.1.0.




















142.....0.1.0.1.0.1.0

A close look at the table reveals certain problems with Turing's own example—not all the symbols are accounted for.

For example, suppose his tape was not initially blank. What would happen? The Turing machine would read different values than the intended values.

2. A copy of Subroutine

This is a very important subroutine used in the "multiply" routine.

The example Turing machine handles a string of 0s and 1s, with 0 represented by the blank symbol. Its task is to double any series of 1s encountered on the tape by writing a 0 between them. For example, when the head reads "111", it will write a 0, then "111". The output will be "1110111".

In order to accomplish its task, this Turing machine will need only 5 states of operation, which are called {s1, s2, s3, s4, s5}. Each state does 4 actions:

  1. Read the symbol under the head
  2. Write the output symbol decided by the state
  3. Move the tape to the left or to the right decided by the state
  4. Switch to the following state decided by the current state
Initial m-configuration (current instruction)Tape symbolPrint operationTape motionFinal m-configuration (next instruction)
s10NNH
s11ERs2
s20ERs3
s21P1Rs2
s30P1Ls4
s31P1Rs3
s40ELs5
s41P1Ls4
s50P1Rs1
s51P1Ls5
H---

A "run" of the machine sequences through 16 machine-configurations (aka Turing states):

SequenceInstruction identifier




Head




1s100001100000
2s200000100000
3s200000010000
4s300000001000
5s400001010000
6s500010100000
7s500101000000
8s100010110000
9s200001001000
10s300000100100
11s300000010010
12s400001100100
13s400011001000
14s500110010000
15s100011011000
16H00011011000

The behavior of this machine can be described as a loop: it starts out in s1, replaces the first 1 with a 0, then uses s2 to move to the right, skipping over 1s and the first 0 encountered. s3 then skips over the next sequence of 1s (initially there are none) and replaces the first 0 it finds with a 1. s4 moves back to the left, skipping over 1s until it finds a 0 and switches to s5. s5 then moves to the left, skipping over 1s until it finds the 0 that was originally written by s1.

It replaces that 0 with a 1, moves one position to the right and enters s1 again for another round of the loop.

This continues until s1 finds a 0 (this is the 0 in the middle of the two strings of 1s) at which time the machine halts.

3. The State Busy Beaver

The following Turing table of instructions was derived from Peterson (1988) page 198, Figure 7.15. Peterson moves the head; in the following model the tape moves.

Tape symbolCurrent state ACurrent state BCurrent state C

Write symbolMove tapeNext stateWrite symbolMove tapeNext stateWrite symbolMove tapeNext state
01RB1LA1LB
11LC1RB1NHALT

The "state" drawing of the 3-state busy beaver shows the internal sequences of events required to actually perform "the state". As noted above Turing (1937) makes it perfectly clear that this is the proper interpretation of the 5-tuples that describe the instruction (Undecidable, p. 119). For more about the atomization of Turing 5-tuples:

location: right

The following table shows the "compressed" run — just the Turing states:

SequenceInstruction identifier





Head






1A00000000000000
2B00000001000000
3A00000110000000
4C00001100000000
5B00011100000000
6A00111100000000
7B00011111000000
8B00001111100000
9B00000111110000
10B00000011111000
11B00000001111100
12A00000111111000
13C00001111110000
14H00001111110000


II. VARIANTS OF TURING MACHINE


* Multitape Turing Machine

A k-tape Turing machine can be described as a 6-tuple M=\langle Q, \Gamma, s, b, F, \delta \rangle where

  • Q is a finite set of states
  • Γ is a finite set of the tape alphabet
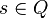  • s \in Q is the initial state
  • b \in \Gamma is the blank symbol
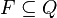  • F \subseteq Q is the set of final or accepting states
  • \delta: Q \times \Gamma^k \rightarrow Q \times (\Gamma \times \{L,R,S\})^k is a partial function called the transition function, where L is left shift, R is right shift, S is no shift.
A multitape TM is like an ordinary TM with several tapes:
  • Each tape has its own head for reading/writing
  • Initially the input is on tape 1 and other are blank
  • Transition function allow for reading, writing,and moving the heads on all tapes simultaneously
Theorem (3.8) 3.13 Every multitape Turing machine has an equivalent single tape Turing machine.

Proof: we show how to convert a multitape TM into a single tape TM. The key idea is to show how to simulate M with S Corollary 3.15 A language is Turing recognizable iff some multitape Turing machine recognizes it

Proof:
  • if: a Turing recognizable language is recognized by an ordinary TM. But an ordinary TM is a special case of a multitape TM.
  • only if: This part follows from the equivalence of a Turing multitape machine with the Turing machine M that simulates it. That is, if L is recognized by M then L is also recognized by the TM s that simulates M.
* Nondeterministic Turing Machines

A nondeterministic Turing machine can be formally defined as a 6-tuple M=(Q, \Sigma, \iota, \sqcup, A, \delta), where

  • Q is a finite set of states
  • Σ is a finite set of symbols (the tape alphabet)
  • \iota \in Q is the initial state
  • \sqcup \in \Sigma is the blank symbol
  • A \subseteq Q is the set of accepting states
  • \delta \subseteq \left(Q \backslash A \times \Sigma\right) \times \left( Q \times \Sigma \times \{L,R\} \right) is a relation on states and symbols called the transition relation.
A non-Deterministic Turing Machine N allows more than one possible action per given state-tape symbol pair. N is always called a non-deterministic recognizer and is said to recognize L(N); furthermore, if in addition for all inputs and all computation branches, N always halts, then N is called a non-deterministic decider and is said to decide L(N).

* Enumerators

A TM with an attached printer.
  • Start with a blank input tape
  • The language enumerated is all the strings it prints out.

* Equivalence with Other Models

Theorem 1.

The following classes of functions are equivalent:
a) the computable functions
b) functions computable by NICE programs, andc) functions computable by SMALL
programs.

Theorem 2.

For every SMALL program there is a Turing machine which computes exact function.
An interesting question about our translation of programs into Turing machinesi nvolves complexity. The previous transformation changed a SMALL programi nto a larger Turing machine and it is obvious that the machine runs for al onger period of time than the program. An intellectually curious reader might work out just what the relationship between the execution times might be.The last step in establishing the equivalence of our three models of computation is to show that NICE programs are at least as powerful as Turing machines. This also will be carried out by a construction, in this case, one that transforms Turing machines into programs.

A Turing machine is equivalent to a Push down automaton that has been made more flexible and concise by relaxing the lat-in-first-out requirement of its stack. (Interestingly, this seemingly minor relaxation enables the Turing machine to perform such a wide variety of computations that it can serve as a clearer model for the computational capabilities of all modern computer software.)

At the other extreme, some very simple models turn out to be Turing-equivalent, i.e. to have the same computational power as the Turing machine model.

Common equivalent models are the multi-tape Turing machine, multi-track Turing machine, machines with input and output, and the non-deterministic Turing machine (NDTM) as opposed to the deterministic Turing machine (DTM) for which the action table has at most one entry for each combination of symbol and state.

Read-only, right-moving Turing Machines are equivalent to NDFA's (as well as DFA's by conversion using the NDFA to DFA conversion algorithm).

For practical and didactical intentions the equivalent register machine can be used as a usual assemblyprogramming language.

0 comments
Subscribe to: Posts (Atom)