CHURCH - TURING THESIS
Posted byA Turing machine is a theoretical device that manipulates symbols contained on a strip of tape. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside of a computer. The "Turing" machine was described by Alan Turing in 1937,who called it an "a(utomatic)-machine". Turing machines are not intended as a practical computing technology, but rather as a thought experiment representing a computing machine. They help computer scientists understand the limits of mechanical computation.
A Turing machine that is able to simulate any other Turing machine is called a Universal Turing Machine (UTM, or simply a universal machine). A more mathematically-oriented definition with a similar "universal" nature was introduced by Alonzo Church, whose work on lamda calculus intertwined with Turing's in a formal theory of computation known as the Chuch Turing Thesis The thesis states that Turing machines indeed capture the informal notion of effective method in logic and mathematics, and provide a precise definition of an algorithm or 'mechanical procedure'.
- Q is a finite set of states
- Σ is an input alphabet, ⊔ / ∈ Σ
- Γ is a tape alphabet, ⊔ ∈ Γ, and Σ ⊂ Γ
- δ : Q × Γ → (Q ∪ {qaccept, qreject}) × Γ × {L,R} is the transition function
- q0inQ is the start state
- qaccept, qreject are the accept and reject states, respectively.
- "1. A machine can be constructed to compute the sequence 0 1 0 1 0 1..." (0
1 0...)
| Configuration | Behavior | ||
|---|---|---|---|
| m-configuration (state) | Tape symbol | Tape operations | Final m-configuration (state) |
| b | blank | P0, R | c |
| c | blank | R | e |
| e | blank | P1, R | f |
| f | blank | R | b |
With regard to what actions the machine actually does, Turing (1936) states the following:
- "This [example] table (and all succeeding tables of the same kind) is to be understood to mean that for a configuration described in the first two columns the operations in the third column are carried out successively, and the machine then goes over into the m-configuration in the final column."
He makes this very clear when he reduces the above table to a single instruction called "b" (Undecidable p. 120), but his instruction consists of 3 lines. Instruction "b" has three different symbol possibilities {None, 0, 1}. Each possibility is followed by a sequence of actions until we arrive at the rightmost column, where the final m-configuration is "b":
| Current m-configuration (instruction) | Tape symbol | Operations on the tape | Final m-configuration (instruction) |
|---|---|---|---|
| b | None | P0 | b |
| b | 0 | R, R, P1 | b |
| b | 1 | R, R, P0 | b |
As observed by a number of commentators including Turing (1937) himself, (e.g., Post (1936), Post (1947), Kleene (1952), Wang (1954)) the Turing instructions are not atomic — further simplifications of the model can be made without reducing its computational power
Turing proposed that his table be further atomized by allowing only a single print/erase followed by a single tape movement L/R/N. He gives us this example of the first little table converted (Undecidable, p. 127):
| Current m-configuration (Turing state) | Tape symbol | Print-operation | Tape-motion | Final m-configuration (Turing state) |
|---|---|---|---|---|
| q1 | blank | P0 | R | q2 |
| q2 | blank | P blank, i.e. E | R | q3 |
| q3 | blank | P1 | R | q4 |
| q4 | blank | P blank, i.e. E | R | q1 |
Turing's statement still implies five atomic operations. At a given instruction (m-configuration) the machine:
- observes the tape-symbol underneath the head
- based on the observed symbol goes to the appropriate instruction-sequence to use
- prints symbol Sj or erases or does nothing
- moves tape left, right or not at all
- goes to the final m-configuration for that symbol
Because a Turing machine's actions are not atomic, a simulation of the machine must atomize each 5-tuple into a sequence of simpler actions. One possibility — used in the following examples of "behaviors" of his machine — is as follows:
- (qi) Test tape-symbol under head: If the symbol is S0 go to qi.01, if symbol S1 go to qi.11, if symbol S2 go to qi.21, etc.
- (qi.01) print symbol Sj0 or erase or do nothing then go to qi.02
- (qi.02) move tape left or right nor not at all then go to qm0
- (qi.11) print symbol Sj1 or erase or do nothing then go to qi.12
- (qi.12) move tape left or right nor not at all then go to qm1
- (qi.21) print symbol Sj2 or erase or do nothing then go to qi.22
- (qi.22) move tape left or right nor not at all then go to qm2
- (etc — all symbols must be accounted for)
So-called "canonical" finite state machines do the symbol tests "in parallel"
In the following example of what the machine does, we will note some peculiarities of Turing's models:
- "The convention of writing the figures only on alternate squares is very useful: I shall always make use of it." (Undecidable p. 121)
Thus when printing he skips every other square. The printed-on squares are called F-squares; the blank squares in between may be used for "markers" and are called "E-squares" as in "liable to erasure." The F-squares in turn are his "Figure squares" and will only bear the symbols 1 or 0 — symbols he called "figures" (as in "binary numbers").
In this example the tape starts out "blank", and the "figures" are then printed on it. For brevity only the TABLE-states are shown here:
| Sequence | Instruction identifier | Head | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | ||
| 1 | 1 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| 2 | 2 | . | . | . | . | . | 0 | . | . | . | . | . | . | . | . | . | . | . | . |
| 3 | 3 | . | . | . | . | . | . | 0 | . | . | . | . | . | . | . | . | . | . | . |
| 4 | 4 | . | . | . | . | . | 1 | . | 0 | . | . | . | . | . | . | . | . | . | . |
| 5 | 1 | . | . | . | . | . | . | 1 | . | 0 | . | . | . | . | . | . | . | . | . |
| 6 | 2 | . | . | . | . | . | 0 | . | 1 | . | 0 | . | . | . | . | . | . | . | . |
| 7 | 3 | . | . | . | . | . | . | 0 | . | 1 | . | 0 | . | . | . | . | . | . | . |
| 8 | 4 | . | . | . | . | . | 1 | . | 0 | . | 1 | . | 0 | . | . | . | . | . | . |
| 9 | 1 | . | . | . | . | . | . | 1 | . | 0 | . | 1 | . | 0 | . | . | . | . | . |
| 10 | 2 | . | . | . | . | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 | . | . | . | . |
| 11 | 3 | . | . | . | . | . | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 | . | . | . |
| 12 | 4 | . | . | . | . | . | 1 | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 | . | . |
| 13 | 1 | . | . | . | . | . | . | 1 | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 | . |
| 14 | 2 | . | . | . | . | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 | . | 1 | . | 0 |
A close look at the table reveals certain problems with Turing's own example—not all the symbols are accounted for.
For example, suppose his tape was not initially blank. What would happen? The Turing machine would read different values than the intended values.
2. A copy of Subroutine
This is a very important subroutine used in the "multiply" routine.
The example Turing machine handles a string of 0s and 1s, with 0 represented by the blank symbol. Its task is to double any series of 1s encountered on the tape by writing a 0 between them. For example, when the head reads "111", it will write a 0, then "111". The output will be "1110111".
In order to accomplish its task, this Turing machine will need only 5 states of operation, which are called {s1, s2, s3, s4, s5}. Each state does 4 actions:
- Read the symbol under the head
- Write the output symbol decided by the state
- Move the tape to the left or to the right decided by the state
- Switch to the following state decided by the current state
| Initial m-configuration (current instruction) | Tape symbol | Print operation | Tape motion | Final m-configuration (next instruction) |
|---|---|---|---|---|
| s1 | 0 | N | N | H |
| s1 | 1 | E | R | s2 |
| s2 | 0 | E | R | s3 |
| s2 | 1 | P1 | R | s2 |
| s3 | 0 | P1 | L | s4 |
| s3 | 1 | P1 | R | s3 |
| s4 | 0 | E | L | s5 |
| s4 | 1 | P1 | L | s4 |
| s5 | 0 | P1 | R | s1 |
| s5 | 1 | P1 | L | s5 |
| H | - | - | - |
A "run" of the machine sequences through 16 machine-configurations (aka Turing states):
| Sequence | Instruction identifier | Head | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | s1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | s2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | s2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4 | s3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5 | s4 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | s5 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | s5 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | s1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 9 | s2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | s3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 11 | s3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 12 | s4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 13 | s4 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 14 | s5 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 15 | s1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 16 | H | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
The behavior of this machine can be described as a loop: it starts out in s1, replaces the first 1 with a 0, then uses s2 to move to the right, skipping over 1s and the first 0 encountered. s3 then skips over the next sequence of 1s (initially there are none) and replaces the first 0 it finds with a 1. s4 moves back to the left, skipping over 1s until it finds a 0 and switches to s5. s5 then moves to the left, skipping over 1s until it finds the 0 that was originally written by s1.
It replaces that 0 with a 1, moves one position to the right and enters s1 again for another round of the loop.
This continues until s1 finds a 0 (this is the 0 in the middle of the two strings of 1s) at which time the machine halts.
3. The State Busy Beaver
The following Turing table of instructions was derived from Peterson (1988) page 198, Figure 7.15. Peterson moves the head; in the following model the tape moves.
| Tape symbol | Current state A | Current state B | Current state C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | |
| 0 | 1 | R | B | 1 | L | A | 1 | L | B |
| 1 | 1 | L | C | 1 | R | B | 1 | N | HALT |
The "state" drawing of the 3-state busy beaver shows the internal sequences of events required to actually perform "the state". As noted above Turing (1937) makes it perfectly clear that this is the proper interpretation of the 5-tuples that describe the instruction (Undecidable, p. 119). For more about the atomization of Turing 5-tuples:
The following table shows the "compressed" run — just the Turing states:
| Sequence | Instruction identifier | Head | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | B | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | A | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | C | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | B | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | A | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | B | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | B | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | B | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 10 | B | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 11 | B | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 12 | A | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 14 | H | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
A k-tape Turing machine can be described as a 6-tuple  where
where
- Q is a finite set of states
- Γ is a finite set of the tape alphabet
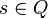 is the initial state
is the initial state is the blank symbol
is the blank symbol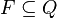 is the set of final or accepting states
is the set of final or accepting states is a partial function called the transition function, where L is left shift, R is right shift, S is no shift.
is a partial function called the transition function, where L is left shift, R is right shift, S is no shift.
- Each tape has its own head for reading/writing
- Initially the input is on tape 1 and other are blank
- Transition function allow for reading, writing,and moving the heads on all tapes simultaneously
Proof: we show how to convert a multitape TM into a single tape TM. The key idea is to show how to simulate M with S Corollary 3.15 A language is Turing recognizable iff some multitape Turing machine recognizes it
Proof:
- if: a Turing recognizable language is recognized by an ordinary TM. But an ordinary TM is a special case of a multitape TM.
- only if: This part follows from the equivalence of a Turing multitape machine with the Turing machine M that simulates it. That is, if L is recognized by M then L is also recognized by the TM s that simulates M.
A nondeterministic Turing machine can be formally defined as a 6-tuple  , where
, where
- Q is a finite set of states
- Σ is a finite set of symbols (the tape alphabet)
 is the initial state
is the initial state is the blank symbol
is the blank symbol is the set of accepting states
is the set of accepting states is a relation on states and symbols called the transition relation.
is a relation on states and symbols called the transition relation.
A TM with an attached printer.
- Start with a blank input tape
- The language enumerated is all the strings it prints out.
A Turing machine is equivalent to a Push down automaton that has been made more flexible and concise by relaxing the lat-in-first-out requirement of its stack. (Interestingly, this seemingly minor relaxation enables the Turing machine to perform such a wide variety of computations that it can serve as a clearer model for the computational capabilities of all modern computer software.)
At the other extreme, some very simple models turn out to be Turing-equivalent, i.e. to have the same computational power as the Turing machine model.
Common equivalent models are the multi-tape Turing machine, multi-track Turing machine, machines with input and output, and the non-deterministic Turing machine (NDTM) as opposed to the deterministic Turing machine (DTM) for which the action table has at most one entry for each combination of symbol and state.
Read-only, right-moving Turing Machines are equivalent to NDFA's (as well as DFA's by conversion using the NDFA to DFA conversion algorithm).
For practical and didactical intentions the equivalent register machine can be used as a usual assemblyprogramming language.





0 comments:
Post a Comment